Problem: Implement Dijkstra's algorithm to find the shortest path between two nodes in a weighted graph.
Dijkstra의 알고리즘을 구현하여 가중치 그래프에서 두 노드 사이의 최단 경로를 찾는다.
Example Input:
graph = {
'A': {'B': 2, 'C': 5},
'B': {'A': 2, 'C': 2, 'D': 1},
'C': {'A': 5, 'B': 2, 'D': 6},
'D': {'B': 1, 'C': 6}
}
start_node = 'A'
end_node = 'D'
Example Output:
Shortest path from A to D: ['A', 'B', 'D']
Shortest distance from A to D: 3Explanation:
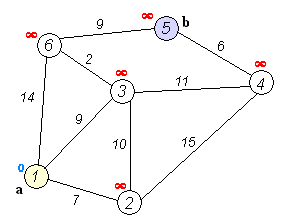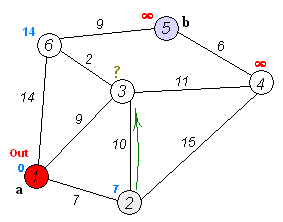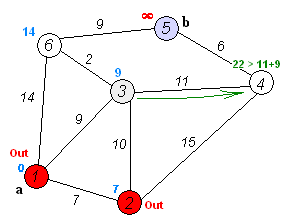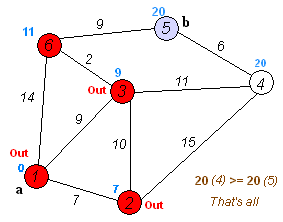
Dijkstra's algorithm is a greedy algorithm that works by repeatedly selecting the node with the smallest distance from the start node and updating the distances of its neighbors. It starts by initializing the distances of all nodes to infinity and the distance of the start node to 0. It then repeatedly selects the node with the smallest distance and updates the distances of its neighbors. It continues this process until it has visited all nodes or until it has visited the end node.
Dijkstra의 알고리즘은 시작 노드에서 거리가 가장 작은 노드를 반복적으로 선택하고
이웃 노드의 거리를 업데이트하는 방식으로 작동하는 그리디 알고리즘.
모든 노드의 거리를 무한대로 초기화하고 시작 노드의 거리를 0으로 초기화하는 것으로 시작.
그런 다음 거리가 가장 작은 노드를 반복적으로 선택하고 이웃 노드의 거리를 업데이트.
모든 노드를 방문하거나 끝 노드를 방문할 때까지 이 프로세스를 반복.
The implementation of Dijkstra's algorithm to solve the above problem in Python is shown below:
Python에서 위의 문제를 해결하기 위한 데이크스트라 알고리즘의 구현은 다음과 같다:
import heapq
def dijkstra(graph, start_node, end_node):
distances = {node: float('inf') for node in graph}
distances[start_node] = 0
queue = [(0, start_node)]
while queue:
current_distance, current_node = heapq.heappop(queue)
if current_node == end_node:
path = []
while current_node != start_node:
path.append(current_node)
current_node = previous_nodes[current_node]
path.append(start_node)
path.reverse()
return path, current_distance
if current_distance > distances[current_node]:
continue
for neighbor, weight in graph[current_node].items():
distance = current_distance + weight
if distance < distances[neighbor]:
# 더 짧은 거리을 찾았을 때
distances[neighbor] = distance
previous_nodes[neighbor] = current_node
heapq.heappush(queue, (distance, neighbor))
return None
학교에서 공부할 땐 딕스트라알고리즘 이라고 배웠었는데
데이크스트라/다익스트라 알고리즘이라고 읽기도 한다.
최단거리 구하는 곳에서 사용되며, 시간복잡도는 O((V+E) log V)
V는 노드의 갯수(the number of vertices)
E는 변의 갯수(the number of edges in the graph)

'IT > 알고리즘' 카테고리의 다른 글
| Depth-First Search (DFS) - 깊이 우선 탐색 (0) | 2023.02.23 |
|---|---|
| Merge Sort - 병합정렬 (0) | 2023.02.16 |
| Binary Search - 이진탐색/이진검색 (0) | 2023.02.16 |



댓글